Finite Difference method
We are starting with the basic numerical Procedure to solve the differetial eqiation which are otherwise very difficult to solve analytically. Finite Difference method can be used to solve the differential equations. For Solving any physical Problem we need to formulate the physical problem in form Governing mathematical eqautions. The solve the governing eqation to get the solution for the problem.
We now consider a simple and classic example for this, The pendulam problem.
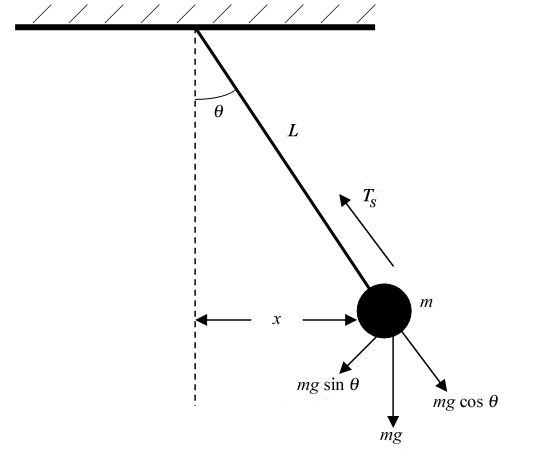
Now writing the Governing Eqaution for this
$$ \begin{align} \vec{\mathbf{F}} = m \vec{a} = \frac{d (m \vec{v})}{d t} \end{align} $$
Now substituting the force values and the velocity vector $$ \begin{align} F_x = -mg \sin \theta \newline v_x = l \frac{d \theta}{dt} \newline \frac{d^2 \theta}{d^2t} + \frac{g}{l} \sin \theta = 0 \end{align} $$ The boundary conditions for this situation are given by $$ \begin{align} \theta _{t=0} = 0 \newline \frac{d \theta}{dt} _{t=0} = v_0 \end{align} $$
Now to solve this Numerically we make an approximations. We first Divide the Domain into node points and then calculate the value of the function at that point and progress similarly.
$$ \begin{align} \frac{d^2 \theta}{dt^2} _{t= t _1} \approx \frac{\theta _{i-1} - 2 \theta _i + \theta _{i+1}} {( \Delta t)^2} \newline \end{align} $$
Thus at time point $t$ we require the values of $ \theta _{N-1}$ and $ \theta _{N+1}$ values. Now at the initial boundary condition the value of $ \theta _{N-1}$ calculated by the specification of boundary condition
$$ \begin{align} \frac{d \theta}{dt} _{t=0} \approx \frac{ \theta _0 - \theta _{-1}}{ \Delta t} = v_0 \end{align} $$
This will lead to a matrix of the varibles and the linear system of equation of form we can solve this equation $$ \begin{align} \mathbf{A} \cdot \theta = \mathbf{B} \end{align} $$
From This we van get the Values of $\theta$ at every point of time. We can choose the $ \Delta t$ difference to calulate the Values of Theta to required accuracy.